
ウォンバット
一番くじ大好き!
でも投資できるお金が有限なのが悩みどころだよね〜。
ということで、一番くじで狙いの賞がでるまでに引く平均期待値の回数を計算するフォームを作成しました(主に自分のために)。
あくまで数学的な確率計算であり、計算結果が実際に試行した場合の回数を保証するものではないことを留意ください。
期待値の計算フォーム
期待値の計算内容

一番くじは、自分より前に購入した人の景品はなくなっている(購入されている)ため、残りのくじの数によって、そこから狙いの賞が出るまでの確率が変動します。
したがって、いわゆる『非復元抽出』の期待値計算をしています。
・『非復元抽出』:抽選する際に、一度抽出したものはその後の対象にならない。
・『復元抽出』:抽出する際に、抽出したものは再び抽出対象に戻してから次の抽選をする。
1. 狙いの賞が残っている場合
まずは具体的に以下の条件で考えてみます。
計算前提:
・狙いの賞:2個
・くじ全体の残りの数:15個(狙いの賞を含む)
・狙いの賞:2個
・くじ全体の残りの数:15個(狙いの賞を含む)
■確率
1回引くだけで狙いの賞があたる確率は、狙いの賞が全体のうち2個あるので、確率は2/15です。
2回連続で引いて狙いの賞があたる確率は、1回目は狙い以外の賞があたり(=(15-2)/15)、2回目で狙いの賞があたる(=2/(15-1))ため、(13/15)*(2/14)です。
3回目、4回目、、、、と同様に計算ができると思います。
1回引くだけで狙いの賞があたる確率は、狙いの賞が全体のうち2個あるので、確率は2/15です。
2回連続で引いて狙いの賞があたる確率は、1回目は狙い以外の賞があたり(=(15-2)/15)、2回目で狙いの賞があたる(=2/(15-1))ため、(13/15)*(2/14)です。
3回目、4回目、、、、と同様に計算ができると思います。
ここで、繰り返し計算を進める計算を一般化します。
あたりがでるまでに連続で引く数をk、箱の中の全体の数をn、狙いの賞の数をmとすると、確率は表のように表すことができます。
あたりがでるまでに連続で引く数をk、箱の中の全体の数をn、狙いの賞の数をmとすると、確率は表のように表すことができます。
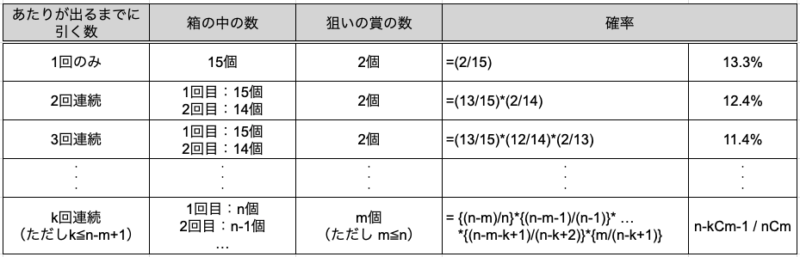
■狙いの賞があたるまでに引く平均回数の期待値
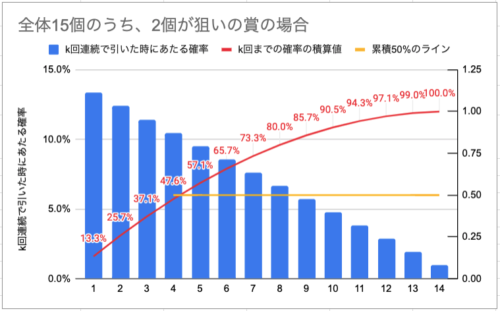
ここでk回連続でくじを引く時の確率の推移をみてみましょう。
青い棒グラフは、k回連続で引いた時にあたる確率を表しており、k回目までその確率を積算したものが赤線のグラフです。
『狙いの賞があたるかあたらないか』は、1/2=50%の確率であるため、狙いの賞があたるまでに引く平均回数の期待値は、『確率の積算値が50%(黄色線)を超える回数』と考えます。
したがってこの計算例の場合は、平均5回連続で引くと狙いの賞が獲得できる、ということになります。
ここでk回連続でくじを引く時の確率の推移をみてみましょう。
青い棒グラフは、k回連続で引いた時にあたる確率を表しており、k回目までその確率を積算したものが赤線のグラフです。
『狙いの賞があたるかあたらないか』は、1/2=50%の確率であるため、狙いの賞があたるまでに引く平均回数の期待値は、『確率の積算値が50%(黄色線)を超える回数』と考えます。
したがってこの計算例の場合は、平均5回連続で引くと狙いの賞が獲得できる、ということになります。
2. 狙いの賞が残っていない場合
狙いの商品が残っていない場合、最後まで購入しても狙いの賞を入手できることはありません。
したがって、狙いの賞があたるまでに引く平均回数の期待値は∞になります。
この計算フォームでの出力結果は『99999』としています。
あとがき

一番くじ『珈琲店 コメダ珈琲店』を購入したかったのですが、発売日の翌日にコンビニを5店舗巡るも全て売り切れでした。
フリマサイトで高価格での出品を見て悲しみつつ、くじの期待値に対してフリマサイトの出品額の妥当性が気になり計算フォームを作成しました。
いろいろな条件で計算してみましたが、やはりフリマサイトの出品額は高い・・・!
転売ヤーに負けずにフリマサイトでは購入しない決心をしました。
自己満足ですが計算フォームが完成して楽しかったです。



コメント